FirWav Real Biorthogonal Filters

• Examples of Individual Filters
• Daubechies Real Biorthogonal Symmetric Spline (DRBSS)
• Daubechies Real Biorthogonal Balanced Regular (DRBBR)
• Daubechies Real Biorthogonal Most Regular (DRBMR)
• Daubechies Real Biorthogonal Most Selective (DRBMS)
• Daubechies Real Biorthogonal Least Uncertain (DRBLU)
• Examples of Filter Families
• Daubechies Real Biorthogonal Symmetric Spline (DRBSS)
• Daubechies Real Biorthogonal Balanced Regular (DRBBR)
• Daubechies Real Biorthogonal Balanced Selective (DRBBS)
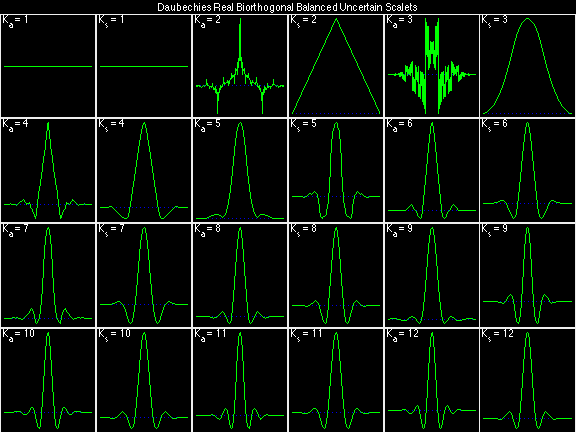
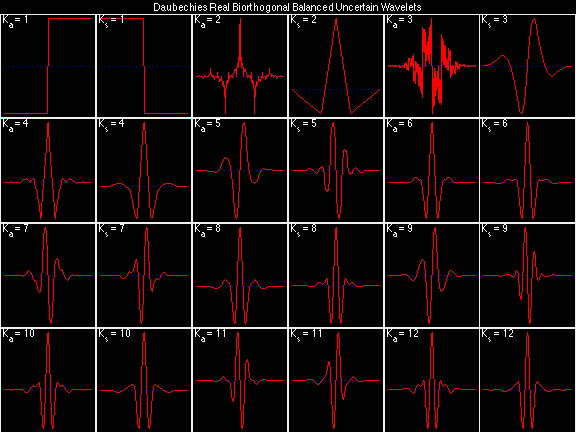
• Daubechies Real Biorthogonal Balanced Uncertain (DRBBU)
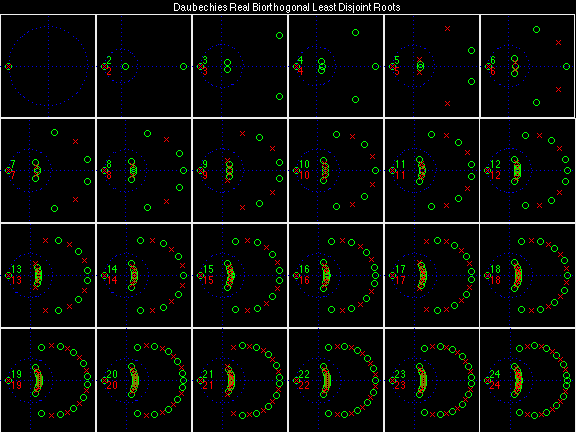
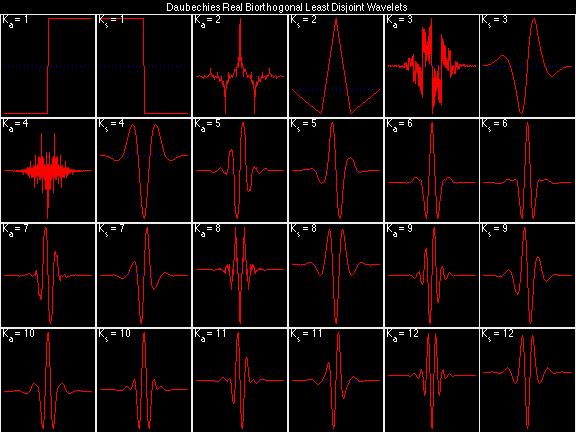
• Daubechies Real Biorthogonal Least Disjoint (DRBLD)
• Daubechies Real Biorthogonal Most Disjoint (DRBMD)
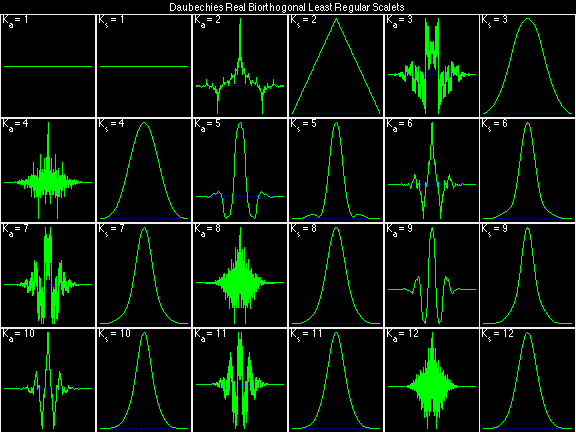
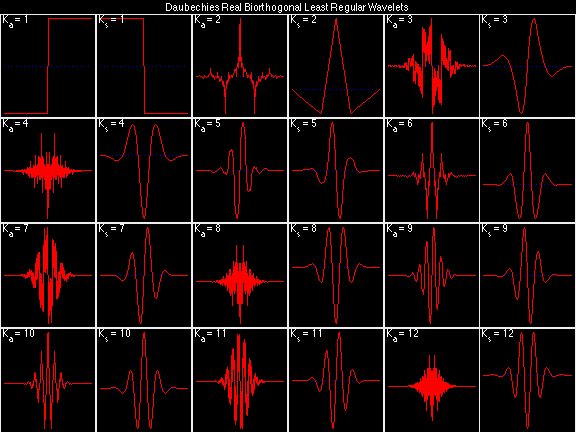
• Daubechies Real Biorthogonal Least Regular (DRBLR)
• Daubechies Real Biorthogonal Most Regular (DRBMR)
• Daubechies Real Biorthogonal Least Selective (DRBLS)
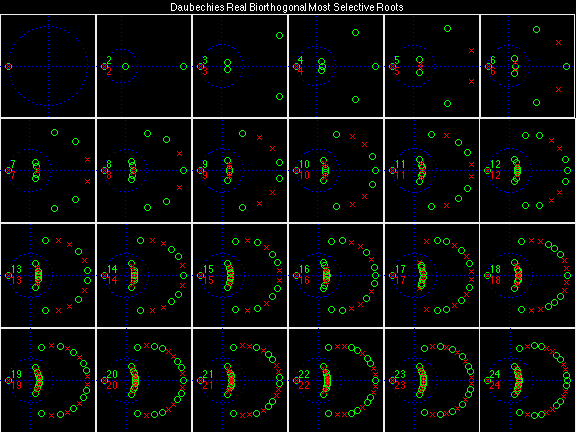
• Daubechies Real Biorthogonal Most Selective (DRBMS)
• Daubechies Real Biorthogonal Least Uncertain (DRBLU)
• Daubechies Real Biorthogonal Most Uncertain (DRBMU)
• Web Site Page Directory

Examples of Individual Filters

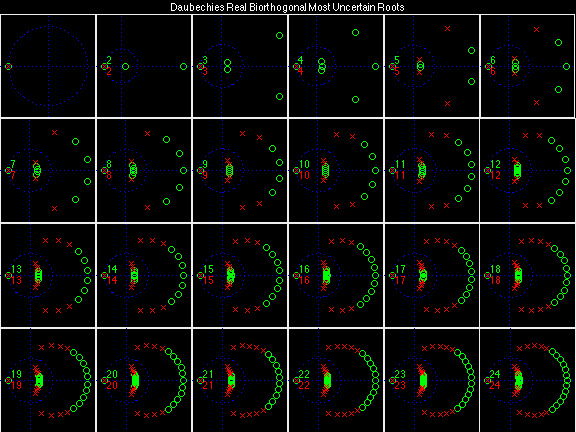
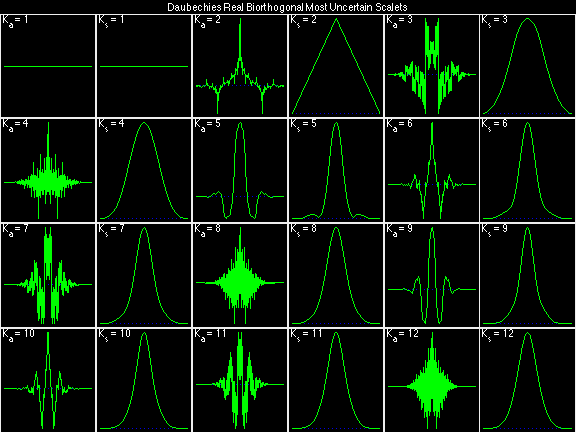
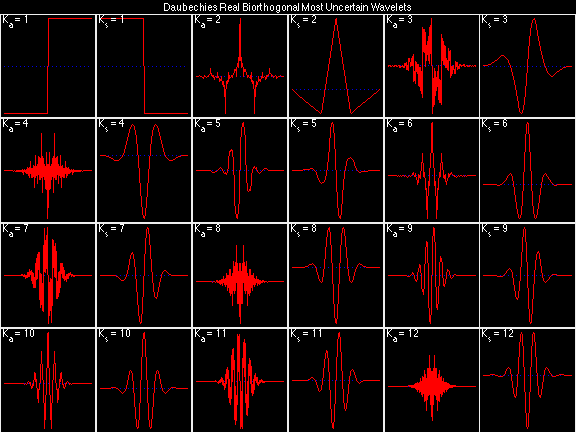
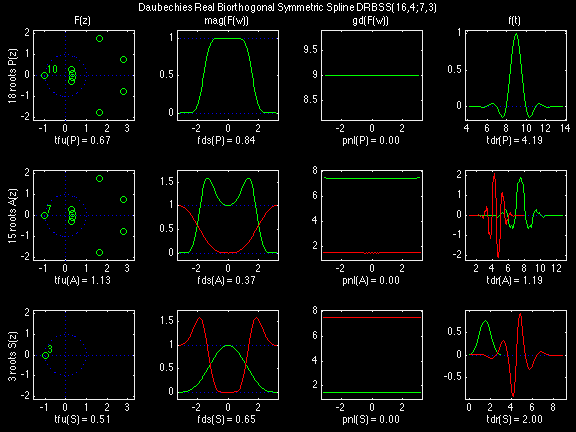
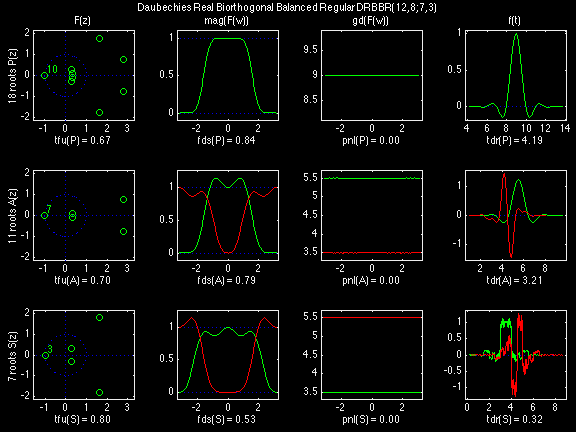
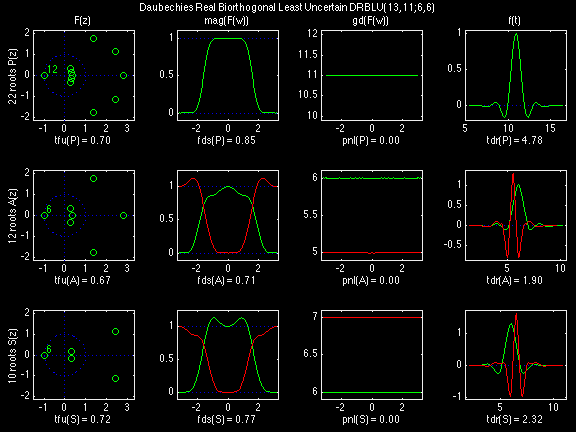
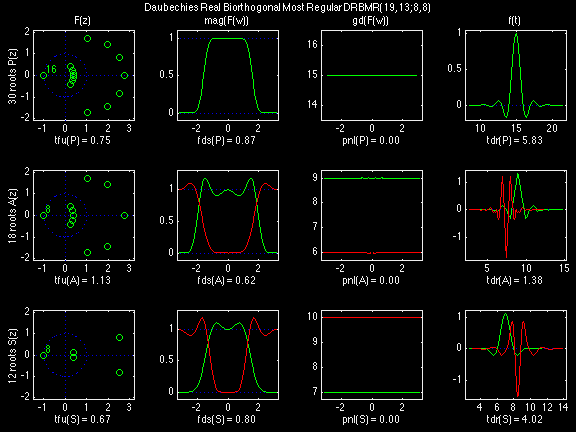
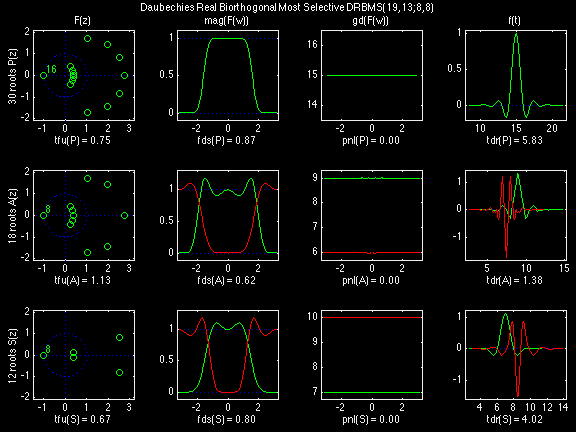
In the following examples of filters, each figure contains a matrix of subplots with rows corresponding to product, analysis, and synthesis filters, and with columns corresponding to characteristics of the filters in the complex z domain, the frequency domain, and the time domain.

Figure legend abbreviations for the plots on this page include:

• f(t) = filter in time t domain;
• F(z) = filter in complex z domain;
• F(w) = filter in frequency w domain;
• mag(F) = magnitude of F(w);
• db(F) = magnitude of F(w) in decibels;
• ang(F) = phase angle of F(w);
• up(F) = unwrapped phase angle of F(w);
• pd(F) = phase delay of F(w);
• gd(F) = group delay of F(w);
• P(z) = Product filter;
• A(z) = Analysis filter, primary spectral factor of P(z);
• S(z) = Synthesis filter, complementary spectral factor of P(z);
• tfu = Time-Frequency Uncertainty;
• tdr = Time-Domain Regularity;
• fds = Frequency-Domain Selectivity; and
• pnl = total Phase NonLinearity.

Scalets (lowpass filters) are in green; wavelets (highpass filters) are in red. In the z domain plots, the number near the zero at z = -1 indicates the multiplicity of that zero. This number determines the theoretical number of vanishing moments of the corresponding wavelet filter.

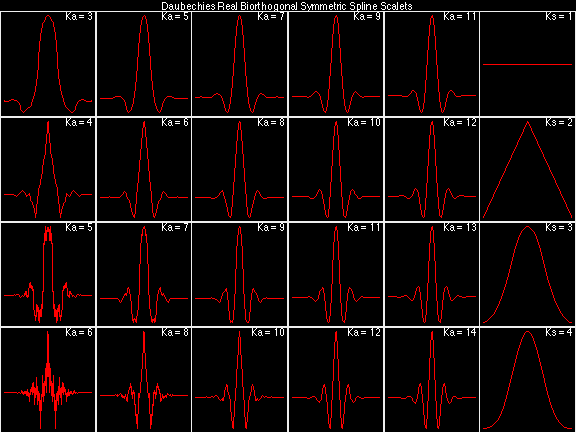
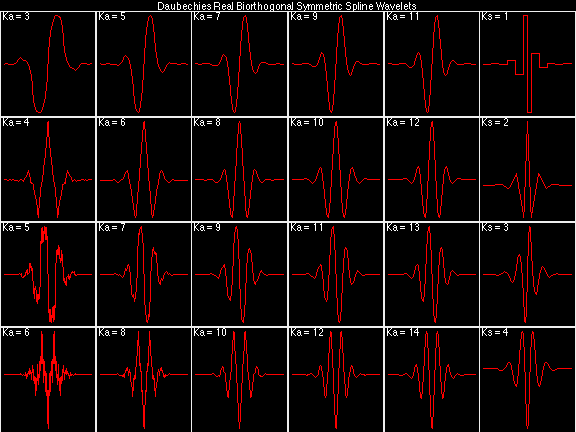
Daubechies Real Biorthogonal Symmetric Spline (DRBSS)

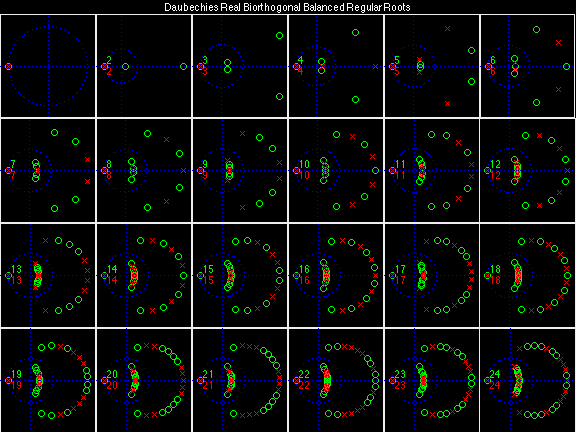
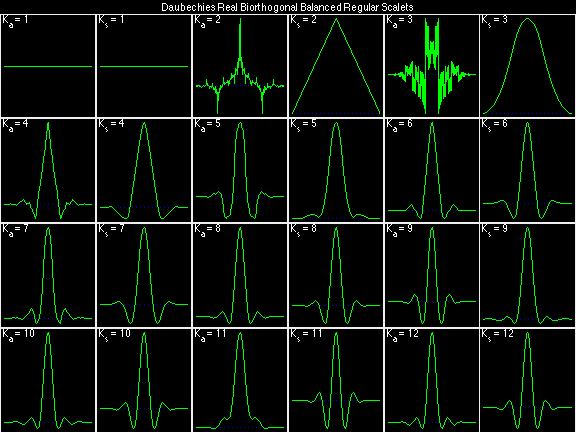
Daubechies Real Biorthogonal Balanced Regular (DRBBR)

Daubechies Real Biorthogonal Least Uncertain (DRBLU)

Daubechies Real Biorthogonal Most Regular (DRBMR)

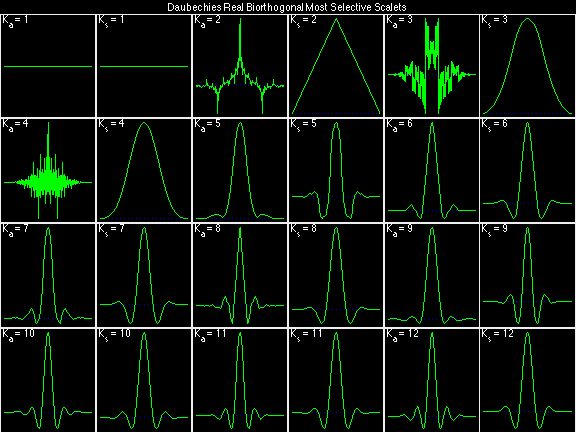
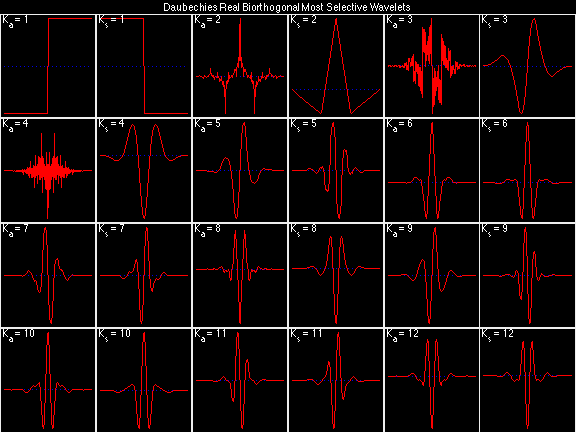
Daubechies Real Biorthogonal Most Selective (DRBMS)

Examples of Filter Families

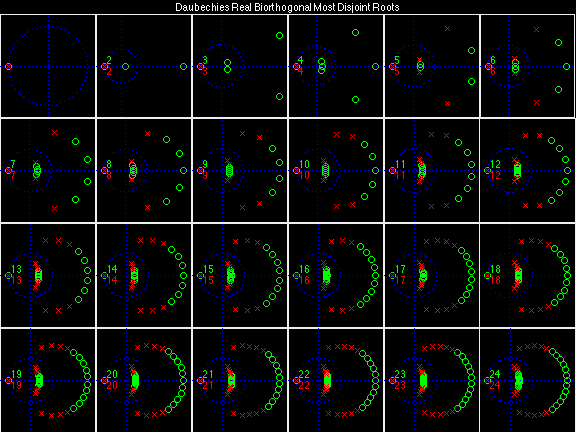
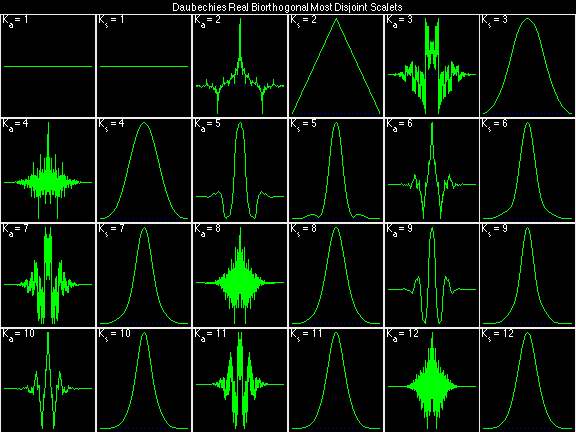
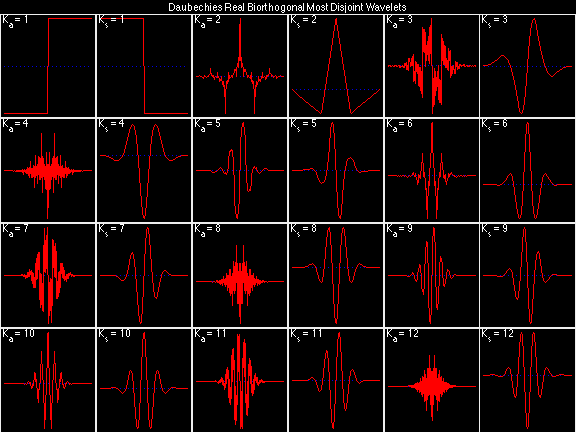
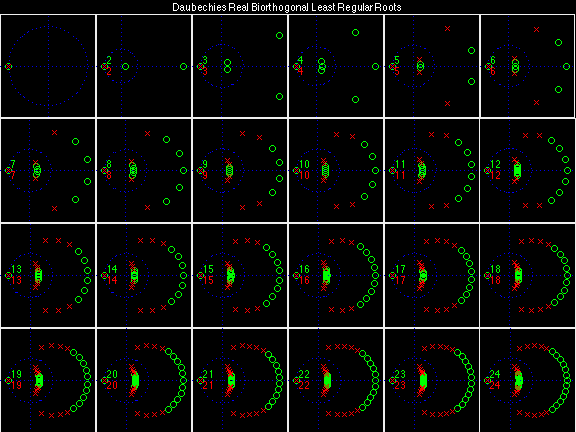
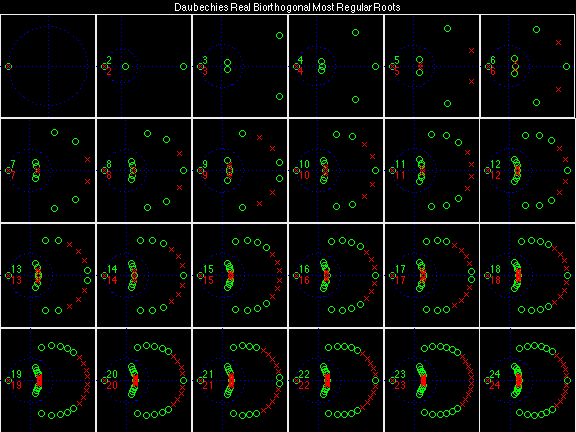
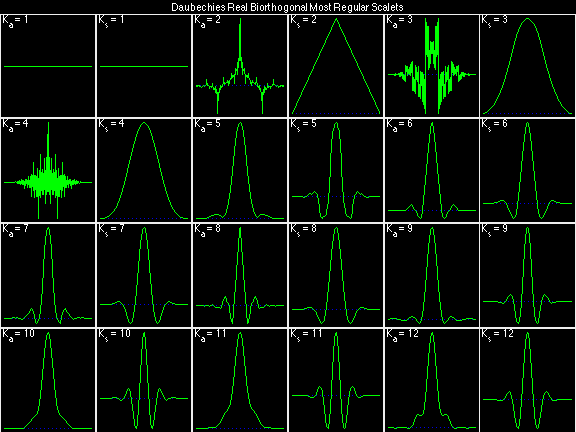
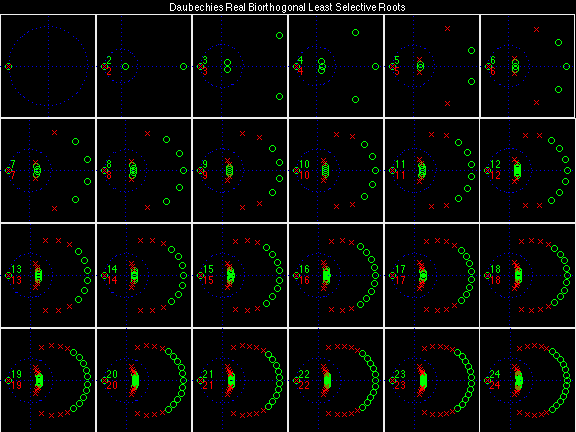
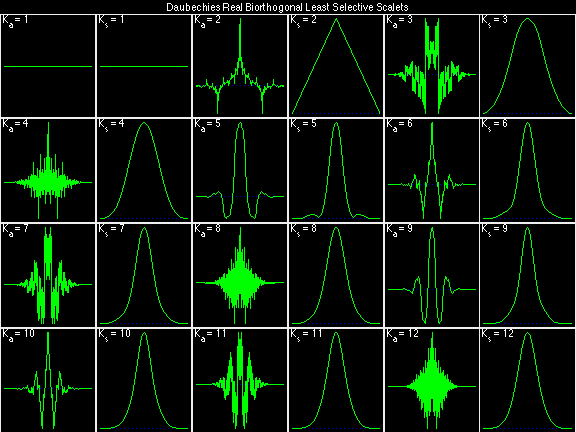
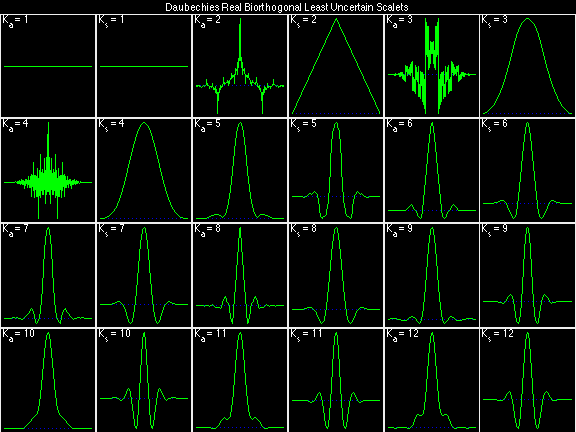
For the DRBSS family, the analysis filters for all values of Ka in each row are paired with the synthesis filter for the value of Ks in the right-most column. For all other biorthogonal families displayed here, each analysis filter is paired with the synthesis filter to its immediate right in the same row. Ka and Ks are the numbers of zeros at z = -1 (w = pi) for the analysis and synthesis scalets which correspond to the numbers of vanishing moments for the synthesis and analysis wavelets, respectively. (The reverse in order of analysis/synthesis for zeros/moments is not a typo.)

Daubechies Real Biorthogonal Symmetric Spline (DRBSS)

Daubechies Real Biorthogonal Balanced Regular (DRBBR)

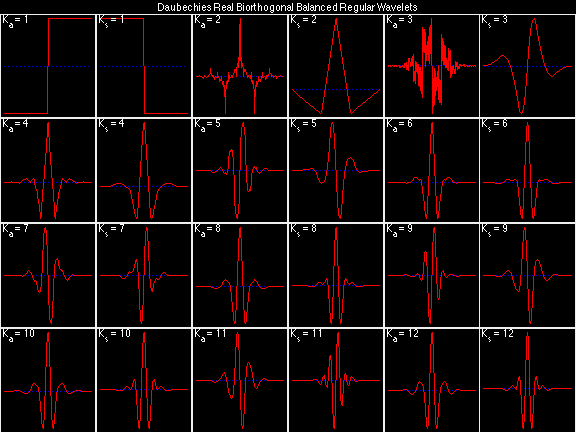
Daubechies Real Biorthogonal Balanced Selective (DRBBS)

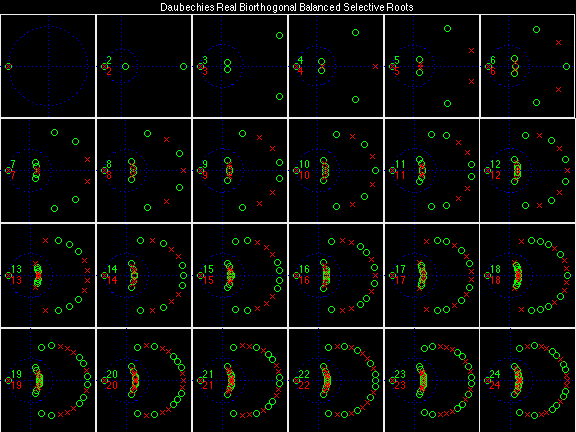
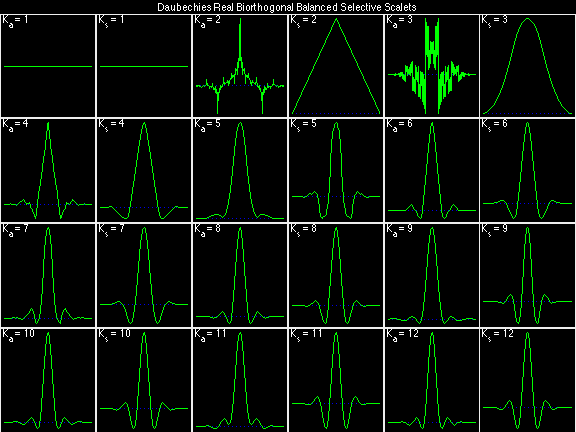
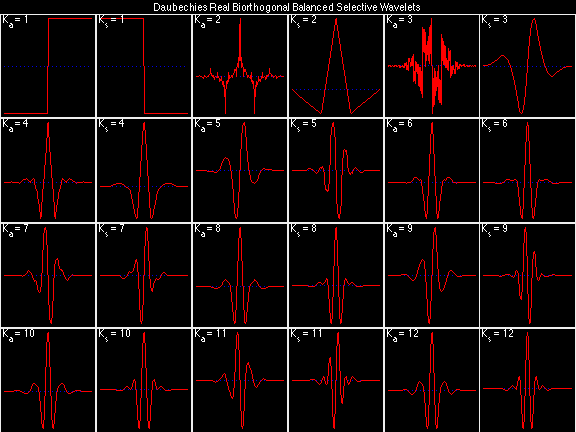
Daubechies Real Biorthogonal Balanced Uncertain (DRBBU)

Daubechies Real Biorthogonal Least Disjoint (DRBLD)

Daubechies Real Biorthogonal Most Disjoint (DRBMD)

Daubechies Real Biorthogonal Least Regular (DRBLR)

Daubechies Real Biorthogonal Most Regular (DRBMR)

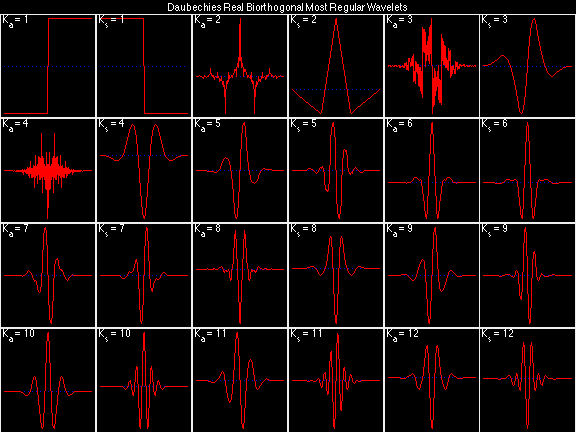
Daubechies Real Biorthogonal Least Selective (DRBLS)

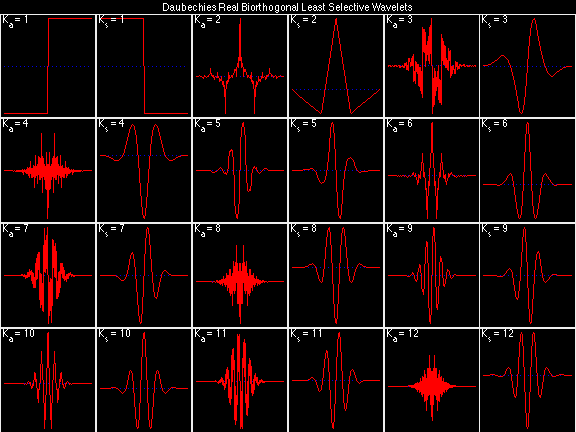
Daubechies Real Biorthogonal Most Selective (DRBMS)

Daubechies Real Biorthogonal Least Uncertain (DRBLU)

Daubechies Real Biorthogonal Most Uncertain (DRBMU)